Note di termodinamica CHIMICA (3)
IL SECONDO PRINCIPIO
Evoluzione dei processi
I processi naturali evolvono in una determinata direzione. Un oggetto, sulla terra, se non sostenuto, tende sempre a cadere verso il basso (perché attratto dalla terra); un gas si espande spontaneamente fino ad occupare tutto il volume a sua disposizione; se un corpo caldo viene messo a contatto con un corpo freddo, fluirà del calore dal corpo più caldo a quello più freddo fino all'equilibrio termico. I processi che evolvono sono termodinamicamente irreversibili (cercheremo di chiarire questa affermazione).
Il primo principio limita il corso dei fenomeni naturali affermando che non è possibile creare o distruggere energia ma solo trasformarla nelle sue diverse forme. Il secondo principio aggiunge ed impone ulteriori limitazioni, in quanto non permette qualsiasi specie di trasformazione, ma solo alcune trasformazioni, ed in determinate condizioni.
Senza voler entrare in particolari tecnici e impegnarci in formule complesse, facciamo un esempio classico: "Mentre è possibile convertire completamente il lavoro meccanico in calore,
per esempio mediante attrito, non è vero l'esatto inverso, cioè la totale conversione del calore in lavoro". Affermiamo quindi che la trasformazione di lavoro in calore è una trasformazione irreversibile. Precisiamo che il termine "irreversibile" non significa che il processo non può essere invertito, indica piuttosto che il processo non può ripercorrere il cammino esattamente in direzione inversa. Se, per esempio, 100 kJ di lavoro sono stati trasformati in 100 kJ di calore, nel processo inverso per ottenere 100 kJ di lavoro occorreranno più di 100 kJ di calore: 100 kJ verranno convertiti in lavoro mentre una certa altra quantità verrà irrimediabilmente dispersa nell'ambiente come afferma l'enunciato di Lord Kelvin:
Enunciato di Lord Kelvin E' impossibile costruire una macchina termica che, assorbendo calore, fornisca una quantità di lavoro equivalente al calore assorbito. (ovvero non esiste il moto perpetuo di seconda specie) |
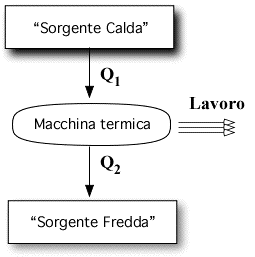 |
Generalizzando, quando un sistema ha subito una trasformazione irreversibile, anche se è vero che è possibile riportare il sistema nelle condizioni iniziali, è altresì vero che rimarrà traccia nell'ambiente di quanto è avvenuto.
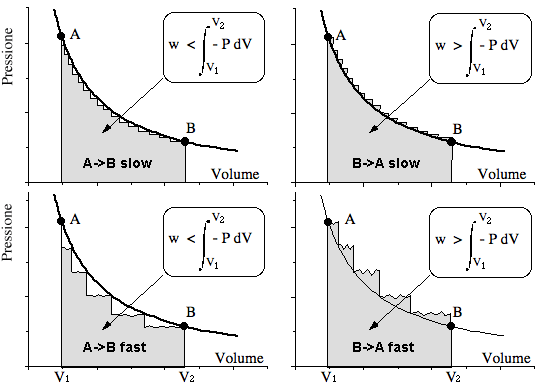
Nella figura precedente è riprodotto il semplice esempio che ho discusso in aula per affermare che i processi reversibili non sono possibili, in quanto un qualunque macroprocesso è costituito da un insieme di piccoli processi irreversibili dovuti ai piccoli squilibri di pressione necessari a provocare la variazione di volume di un gas. Nel processo isotermo rappresentato è impossibile percorrere esattamente l'iperbole (percorso ideale) seppur ci si può avvicinare tantissimo ad essa utilizzando squilibri infinitesimi (parte superiore dell'immagine). Vi ricordo ancora che per far tornare il sistema allo stato iniziale (A), si percorrerà una strada diversa rispetto a quella fatta andando da (A) verso (B). In altri termini sarà necessario un lavoro (area grigia sottostante) maggiore di quello fatto dal sistema durante il percorso (A->B) per riportarlo alle condizioni iniziali con il percorso (B->A). L'ambiente si impoverisce di energia ad ogni ciclo (A->B->A) tanto più quanto più la trasformazione ciclica assume un maggior carattere di irreversibilità (squilibri meno graduali nella parte inferiore della figura).
Ricordatevi che i termini "reversibile" e "irreversibile" non si riferiscono al solo sistema, ma all'insieme di sistema-ambiente.
ENTROPIA e direzione di un processo
( L'universo tende verso il massimo disordine? )
Lo scopo della termodinamica è quello di prevedere la direzione di un processo una volta che siano note le condizioni sperimentali. Spesso si dice che i sistemi tendono ad evolvere verso uno stato di minima energia potenziale. Ma questo criterio non risolve tutti i problemi e spesso è contraddetto. Occorre trovare una funzione di stato del sistema capace di controllare:
| a) | L'irreversibilità (spontaneità ad avvenire) di un processo | |
| b) | la preferenza per lo stato termodinamico più probabile | |
| c) | Il “disordine” (non nel senso qualitativo del termine ma correlato alla organizzazione strutturale del sistema, al suo grado di omogeneità e alla sua temperatura) |
Questa Grandezza fu trovata nel 1864 da Rudolf Clausius, la chiamò ENTROPIA e ne propose la formulazione matematica
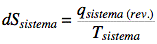
La formulazione di Clausius non è di immediata applicazione come suggerirebbe la semplicità apparente, ma consente il calcolo dell'entropia e della sua variazione seguendo percorsi reversibili ideali.
L'entropia, se riferita ad un sistema o a una sostanza chimica, è una grandezza estensiva e dipende dalla temperatura. Essa tende globalmente sempre ad aumentare e mai a diminuire: se si riscontra una diminuzione di entropia in un sistema, significa l'ambiente circostante ha avuto un incremento di entropia che supera certamente la diminuzione osservata nel sistema. In altri termini tutti i processi spontanei (ovvero "che avvengono") sono caratterizzati da un aumento di entropia totale, dove con questo termine intendiamo la somma dell'entropia del sistema e dell'ambiente del sistema:
| ΔStotale = ΔSsistema + ΔSambiente | 3.1 |
Così il secondo principio è divenuto il principio dell'aumento dell'entropia e qualcuno lo enuncia nel modo seguente: in un sistema isolato ogni trasformazione spontanea (irreversibile) è accompagnata da un incremento dell'entropia totale e non possono verificarsi trasformazioni che comportino, all'inverso, una diminuzione di entropia totale.
I processi reversibili sono quelli per cui la variazione di entropia è nulla. Sono cioè processi che non avvengono, ovvero non modificano la loro condizione perchè si trovano in una situazione di equilibrio. Alcune volte si legge di processi condotti reversibilmente e si dice che si tratta di processi condotti attraverso stati di equilibrio successivi mediante perturbazioni infinitesime e che quindi richiedono un tempo infinito. Se per una causa esterna il processo si muove rispetto alla situazione di equilibrio, assume, anche se per una piccolissima quantità, carattere di irreversibilità. In pratica i processi reversibili non esistono, sono solo delle astrazioni matematiche molto utili per effettuare calcoli termodinamici.
Ludwig Boltzman (1844-1906) ha associato il concetto di entropia a quello di probabilità di stato. La probabilità di stato è calcolabile mediante metodi statistici e determina quantitativamente il termine “preferenza”, in verità abbastanza vago, che ho usato precedentemente.
Si osserva che la natura preferisce uno stato più probabile ad uno meno probabile, e compie spontaneamente solo quei passaggi che avvengono nella direzione della maggiore probabilità e, perlomeno nel mondo in cui viviamo, l'evento altamente improbabile non si verifica mai spontaneamente.
Uno studio statistico completo sull’argomento dovrebbe riguardare un grande numero di individui. Per spiegare il concetto io mi limiterò ad utilizzare un numero assai piccolo di oggetti, criticabile, ma che chiarisce, seppur in maniera qualitativa, il concetto di probabilità di stato.
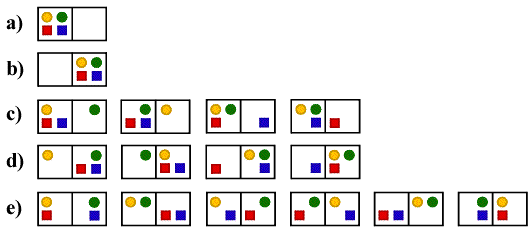
Supponiamo di avere 4 particelle indistinguibili (che noi distingueremo per nostra comodità utilizzando cerchi, quadrati e colori) e di volerle distribuire su due sole posizioni (spazio destro e spazio sinistro senza tener conto della disposizione all'interno degli spazi che supporremo equivalenti). Le quattro particelle potranno distribuirsi in 24=16 configurazioni diverse.
In base alle configurazioni possiamo definire con il termine MICROSTATO un certo tipo di configurazione equiprobabile:
|
a) distribuzione totalmente a sinistra b) distribuzione totalmente a destra c) distribuzione con prevalenza a sinistra d) distribuzione con prevalenza a destra e) equa distribuzione |
Ecco la formulazione di Boltzmann:
| S = k ln(w) | 3.2 |
in cui k è la costante di Boltzmann, pari alla costante universale dei gas diviso il numero di Avogadro (k=R/NA = 1.38.10-23 J K-1) e w (omega) è la probabilità di stato. "La probabilità di stato è funzione del numero di microstati possibili, dipende dalle dimensioni del sistema, dal numero di particelle e dal numero di disposizioni possibili". La probabilità di stato viene spesso indicata brutalmente con il termine "disordine" che essendo sinonimo di "confusione, caos, disorganizzazione" può ingenerare cattive interpretazioni di un concetto che deve essere associato alla descrizione strutturale di un sistema. Nei cristalli perfetti ci sono geometrie prestabilite e la probabilità di stato è bassa (le disposizioni sono praticamente fisse); di conseguenza anche l'entropia è bassa. A questo proposito si consideri come esempio un campione di NaCl solido cristallino perfetto. Ad una certa temperatura la sua entropia molare è bassa, maggiore del Sodio metallico puro che ha maggiore omogeneità strutturale. Se il cristallo di NaCl viene sciolto in acqua, si avrà un grande aumento di entropia in quanto aumenta enormemente la probabilità di stato a causa della dispersione ionica (un gran numero di ioni liberi in soluzione) e all'occupazione di un volume molto più grande (l'intero volume della soluzione).
Esempi di processi spontanei (ovvero che avvengono)
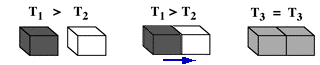 1) Consideriamo un sistema isolato costituito da due corpi a temperatura diversa; se posti a contatto, una certa quantità di calore passerà dal corpo a temperatura più alta al corpo a temperatura più bassa fino al raggiungimento dell'equilibrio termico. Il motivo di questo processo spontaneo è da ricercarsi nel fatto che lo stato di uguale distribuzione della temperatura è più probabile di ogni stato di ineguale distribuzione di temperatura (ricordo il concetto di equa distribuzione).
A ciò corrisponde un aumento di Entropia, dovuto alla degradazione dell'energia rappresentata dalla perdita della capacità di utilizzare il dislivello di temperatura per compiere lavoro (la quantità totale di energia del sistema rimane costante).
1) Consideriamo un sistema isolato costituito da due corpi a temperatura diversa; se posti a contatto, una certa quantità di calore passerà dal corpo a temperatura più alta al corpo a temperatura più bassa fino al raggiungimento dell'equilibrio termico. Il motivo di questo processo spontaneo è da ricercarsi nel fatto che lo stato di uguale distribuzione della temperatura è più probabile di ogni stato di ineguale distribuzione di temperatura (ricordo il concetto di equa distribuzione).
A ciò corrisponde un aumento di Entropia, dovuto alla degradazione dell'energia rappresentata dalla perdita della capacità di utilizzare il dislivello di temperatura per compiere lavoro (la quantità totale di energia del sistema rimane costante).
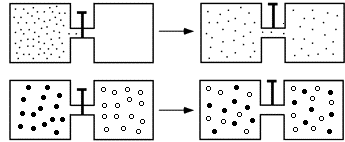 2) Un gas si espande contro il vuoto perché ciò è molto più probabile piuttosto che il processo avvenga all'inverso, cioè con la raccolta delle molecole del gas in un unico recipiente, data la bassissima probabilità che tutte le velocità concorrano a tale ritorno.
Oppure: il peso statistico delle distribuzioni spaziali è maggiore quando le molecole si disperdono in uno spazio maggiore dando origine ad una occupazione media equa di tutto lo spazio disponibile per un maggior numero di distribuzioni possibili. Espandendosi contro il vuoto il gas non compie lavoro e l'energia del sistema rimane costante.
2) Un gas si espande contro il vuoto perché ciò è molto più probabile piuttosto che il processo avvenga all'inverso, cioè con la raccolta delle molecole del gas in un unico recipiente, data la bassissima probabilità che tutte le velocità concorrano a tale ritorno.
Oppure: il peso statistico delle distribuzioni spaziali è maggiore quando le molecole si disperdono in uno spazio maggiore dando origine ad una occupazione media equa di tutto lo spazio disponibile per un maggior numero di distribuzioni possibili. Espandendosi contro il vuoto il gas non compie lavoro e l'energia del sistema rimane costante.
Il mescolamento spontaneo di due gas diversi può essere inquadrato come doppia espansione spontanea a cui si aggiunge un aumento delle distribuzioni possibili dovute alla presenza dell’altro gas che introduce ulteriore possibilità di scambi di posizione.
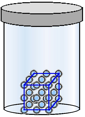
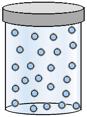
3) A parità di numero di moli e nelle stesse condizioni di temperatura e pressione, l'entropia di una specie chimica allo stato aeriforme è certamente superiore a quella della stessa specie allo stato liquido, che sarà ancora superiore a quella della sostanza allo stato solido. Questo fatto è razionalmente inquadrabile se si pensa alla diminuzione dell'organizzazione strutturale (ordine?) a causa della diminuzione dell'aggregazione e nella maggiore libertà di movimento nel passaggio da stati più condensati a quelli meno condensati.
Ssolido |
< | Sliquido |
< | Svapore |
 |
 |
 |
||
Solido |
Liquido |
Aeriforme |
Attenzione all'ambiente del sistema
Soffermiamoci un attimo sul passaggio di stato solido-liquido e consideriamo il semplice sistema costituito da una certa quantità di acqua solida. Possiamo dire che la variazione di entropia del sistema nel passaggio solido-liquido (fusione) è sicuramente maggiore di zero (ΔSsistema>0 ) mentre per il passaggio inverso è ΔSsistema<0; affermare la stessa cosa nei riguardi dell'entropia senza specificare che si sta considerando solo il sistema non è corretto (ΔS>0 o ΔS<0).
A) |
|
B) |
|
Ma allora, è spontaneo il passaggio solido-liquido o quello inverso? La spiegazione ai due fenomeni "spontanei" non può fare a meno di prendere in considerazione il contorno ambientale, senza limitarsi ad osservare solamente quanto accade nel sistema. Nella fusione spontanea (A) il sistema, che si trova a contatto con un ambiente ad una temperatura superiore
a 273.15 K
ed acquista calore da quest'ultimo: l'ambiente pertanto diminuisce la sua entropia ma il sistema aumenta la propria di una quantità superiore e complessivamente il processo conduce ad un aumento di entropia (processo spontaneo). Nel secondo caso (B), è certamente vero che il sistema diminuisce la propria entropia nel passaggio liquido-solido, ma il calore che viene acquistato dall'ambiente (che si trova ad una temperatura inferiore
a 273.15 K
) produce in quest'ultimo un aumento di entropia superiore ed alla fine il bilancio globale consiste in un aumento di entropia totale. In definitiva i due processi sono entrambi spontanei perchè in tutti e due i casi si è verificato un aumento di entropia globale.
Negli organismi viventi l’ordine interno, in termini di organizzazione strutturale, è accresciuto e mantenuto mediante il prelievo di energia libera dall’ambiente circostante (attraverso i nutrienti nel caso di cellule eterotrofiche, o attraverso la radiazione della luce solare nel caso di cellule fotosintetiche), e restituendo all’ambiente energia ed entropia, in perfetto accordo con la seconda legge della termodinamica sull'incremento globale dell'entropia.
Terzo principio della Termodinamica
Ogni specie chimica ha un'entropia finita e positiva, che è una funzione crescente con la temperatura e che con il tendere della temperatura allo zero assoluto tende ad un valore minimo, valore che diventa zero nel caso di sostanze cristalline che siano cristalli perfetti.
In base al terzo principio è possibile determinare le entropie assolute delle sostanze ad una certa temperatura e pressione, con un minimo errore dovuto all'entropia residua allo zero assoluto per le sostanze che non sono cristalli perfetti.
La determinazione delle entropie assolute nelle condizioni standard (25°C e 1 Bar), generalmente riferite ad una mole di sostanza, è fatta valutando il risultato di una serie di esperimenti. L'entropia non può essere misurata direttamente perchè non esiste uno strumento che possa misurarla (l'ipotetico entropimometro). Il metodo utilizzato deriva dalla definizione di Clausius dell'entropia (vi risparmierò la parte teorica),
A titolo di esempio, per valutare l'entropia molare assoluta della glicina, viene determinato sperimentalmente, un discreto numero di volte, il calore specifico molare (Cp) di questa sostanza a partire dalla temperatura più bassa possibile fino a quella standard di 298.15 kelvin. L'entropia della glicina, a 298.15 kelvin, risulta essere l'area che sottende alla curva ottenuta mettendo in grafico Cp/T vs. T, estesa da 0 a 298.15 kelvin. L'unica incertezza, abbastanza piccola, riguarda solo la primissima parte dell'area.
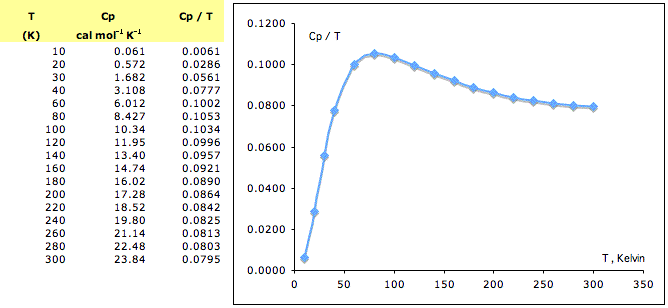
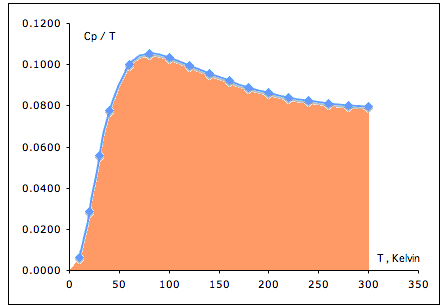
Il caso presentato riguarda una sostanza che si mantiene solida fino alla temperatura di 298.15 K, pertanto non sono presenti discontinuità nelle curve sperimentali di sostanza cheprevedono transizioni di fase.
Le entropie in condizioni standard degli ioni in soluzione sono valori relativi ad uno zero convenzionale stabilito, analogamente a quanto fatto per l'entalpia, per lo ione H+ aquoso.
Variazioni di entropia nelle reazioni chimiche
La variazione di entropia del sistema “reazione” è data dalla differenza di entropia dei prodotti e quella dei reagenti tenendo conto dei coefficienti stechiometrici. Generalmente si utilizza la variazione standard e pertanto si prelevano i valori di entropia tabulate in tali condizioni.
| ΔS°reaz. = Σ ( νprod. S°prod. ) - Σ ( νreag. S°reag. ) | 3.1 |
L'ambiente, nell'ipotesi di temperatura costante, modificherà la propria entropia in senso inverso alla tonalità termica della reazione e questa variazione vale all'incirca quello della tonalità termica diviso la temperatura dell'ambiente che deve trovarsi alla temperatura standard di 298 K.
| ΔS°ambiente = (- ΔH°reaz. / T° ) | 3.2 |
La spontaneità o meno del processo dipende dal segno dell’entropia totale:
| ΔStotale = ΔS°reaz. + ΔS°ambiente |
3.3 |
|
3.4 |
Si consideri ad esempio la seguente reazione (in basso le S° delle specie chimiche):
| H2 (g) | + | 0.5 O2 (g) | H2O (g) | ΔS°reaz.= - 44.4 J mol-1 K-1 | ||
| 130.6 | 205/2 | 188.7 |
La variazione di entropia del sistema reazione risulta negativa (diminuisce nel passaggio da reagenti a prodotti) soprattutto per la riduzione del numero di particelle. Si potrebbe dedurre che il processo non sia spontaneo. Come è noto, invece, Il processo è spontaneo (anche se necessita di attivazione per essere osservabile). Il motivo della spontaneità del processo è dovuto al fatto che ha un ΔH molto negativo e ciò incrementa l'entropia dell'ambiente rendendo molto positiva la variazione totale di entropia.
|
Note sulle tabelle di entropie molari standard.
a) Per le sostanze chimiche si osservano solo valori positivi
b) S°gas >> S°liquido > S°solido
c) Gli ioni in soluzione possono avere valori negativi.
d) Tende ad aumentare con la massa (es. F2<Cl2<Br2<I2)
d) Tende ad aumentare con la complessità struttrale. Esempi:
S°KCl < S°CaCl2 < S°GaCl3
S°metano < S°etano < S°propano < S°n-butano
 Se si tira fuori dal congelatore un contenitore con acqua ghiacciata, dopo un poco si osserva che "spontaneamente" il ghiaccio diventa liquido.
Se si tira fuori dal congelatore un contenitore con acqua ghiacciata, dopo un poco si osserva che "spontaneamente" il ghiaccio diventa liquido. Se si ripone il contenitore nel congelatore, dopo un certo tempo si riforma "spontaneamente" il ghiaccio.
Se si ripone il contenitore nel congelatore, dopo un certo tempo si riforma "spontaneamente" il ghiaccio.