Forme degli orbitali atomici
Gli orbitali sono funzioni matematiche che non hanno alcun significato fisico ma permettono di ricavare le funzioni di probabilità di rintracciare l'elettrone (ψ2).
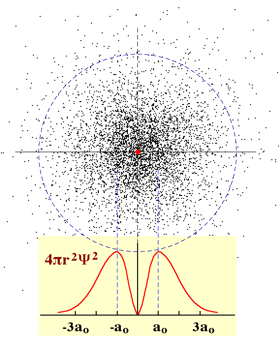
La figura mostra il modello di un atomo di idrogeno in una sezione passante per il nucleo. Viene
visualizzata la mappa di densità di probabilità dell'orbitale 1s con il nucleo colorato in rosso (molto ingrandito per individuarlo).
Il criterio utilizzato è il seguente: maggiore è la probabilità di trovare l'elettrone in una certa zona dello spazio e più fitta sarà
la trama dei punti in quella zona.
Gli orbitali "s" sono caratterizzati da una simmetria sferica, cioè la probabilità di rintracciare l'elettrone dipende dalla distanza dal nucleo in modo indipendente dalla direzione.
Nella parte inferiore della figura (sfondo giallo) è tracciata la funzione relativa alla cosiddetta densità di probabilità radiale (4π r2ψ2); ha valore praticamente nullo sul nucleo, cresce fino a 53 pm (1a0) per tornare a diminuire man mano che ci si allontana dal nucleo. Nel caso dell'orbitale 1s, per distanze maggiori di 3a0, la probabilità di trovare l'elettrone diventa piuttosto piccola e così anche la densità di probabilità radiale.
Usualmente, per motivi estetici e soprattutto pratici, le forme orbitaliche vengono tracciate considerando superfici
di uguale probabilità all'interno delle quali è molto probabile rintracciare l'elettrone; viene spesso indicato il segno della funzione orbitale originaria. Nella figura che segue (lato sinistro) la forma orbitalica 1s viene raffigurata come una sfera con segno positivo (blu) perchè positivo è il segno della funzione d'onda orbitale che ha permesso di definire la densità di probabilità:
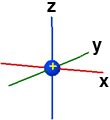 1s ψ(1,0,0) |
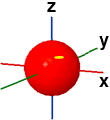 2s ψ(2,0,0) |
Gli orbitali "s" dei livelli superiori (2s, 3s, etc.), pur avendo simmetria sferica, hanno una distribuzione della probabilità radiale con sfere interne come superfici nodali (probabilità nulla di trovare l'elettrone). In particolare la forma orbitalica 2s deriva da una funzione d'onda positiva vicino al nucleo e negativa nella parte esterna: ecco perchè viene rappresentata da una sfera più grande accompagnata da un segno meno (rosso).
|
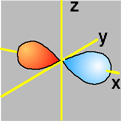
Le forme orbitaliche "2p" non hanno simmetria sferica ma hanno una forma caratterizzata da due lobi. Sono presenti tre orbitali "p" per ogni livello energetico superiore al primo. I due lobi di ciascuna forma orbitalica "2p" si estendono lungo i tre assi x, y e z (prendono il nome rispettivamente 2px, 2py, 2pz). A sinistra, premendo i relativi radio-button di selezione si potranno osservare i tre orbitali p stilizzati, sia separatamente che tutti insieme. Sono stati resi più sottili proprio per poterli ben visualizzare se presenti tutti e tre contemporaneamente. |
Nella figura seguente vengono rappresentate le tre forme orbitaliche "2p" meno stilizzate, separatamene e tutte tre insieme; il diverso segno della funzione orbitale originaria viene indicato dalla colorazione (blu=positivo, rosso=negativo). Gli orbitali 2p hanno delle superfici piane di tipo nodale. Per evidenziare i piani nodali utilizzare il pulsantino check (on/off) sul lato destro.
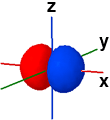
2px ψ(2,1,+1) |
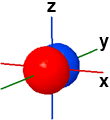
2py ψ(2,1,-1) |
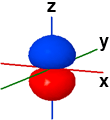
2pz ψ(2,1,0) |
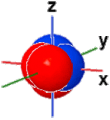 2px + 2py + 2pz |
Le forme orbitaliche "p" dei livelli superiori a 2, pur estendendosi ancora preferenzialmente lungo i tre assi, presentano sia il solito piano nodale all'incrocio degli assi che altre superfici nodali.
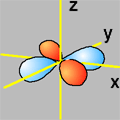
La forma dei cinque orbitali "d" è più complessa e in questa sede faremo riferimento solo agli orbitali 3d. Quattro orbitali "3d" presentano quattro lobi diretti ai vertici di un quadrato: il loro nome deriva dal piano assiale di referimento che taglia esattamente a metà tutti e quattro i lobi. Due di questi quattro orbitali, Il dxy e il dx2-y2, fanno riferimento allo stesso piano (x-y) ma sono ruotati di 45° l'uno rispetto all'altro. Il rimanente quinto orbitale "d", il dz2, ha un doppio lobo che si estende lungo l'asse z e una corona toroidale attorno al centro, sul piano x-y.
|
A sinistra, premendo i relativi radio-button di selezione si potranno osservare in sequenza i cinque orbitali "3d" stilizzati, sia separatamente che tutti insieme. Anche se stilizzati, quando sono illustrati tutti insieme assumono una forma complessiva quasi sferica. La figura che segue li rappresenta staticamente meno stilizzati. Per visualizzare i piani di riferimento utilizzare il pulsantino check (on/off) posizionato in basso a destra. |
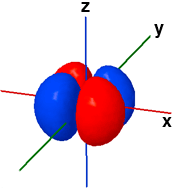
3dxy ψ(3,2,1) |
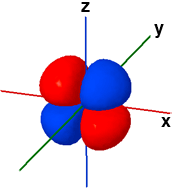
3dxz ψ(3,2,2) |
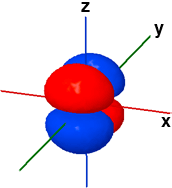
3dyz ψ(3,2,-1) |
t2g |
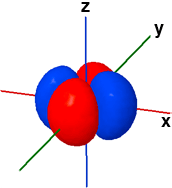
3dx2-y2 ψ(3,2,-2) |
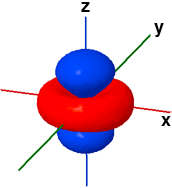
3dz2 ψ(3,2,0) |
eg |
NOTE e approfondimenti interattivi:
Alcune soluzioni equazione d'onda; coordinate polari
Tabella grafici densità di probabilità
IsoSurface di orbitali 2s e 2p (JSmol)
IsoSurface di orbitali 3d (JSmol)
Rappresentazione densità di probabilità in densità di punti JSmol)
Link verso internet:
http://undergrad-ed.chemistry.ohio-state.edu/bonding/index.html
http://winter.group.shef.ac.uk/orbitron/