Elettroliti in soluzione (1)
 |
 |
 |
 |
| Alessandro Volta (Italy) 1745-1827 | Georg Simon Ohm (Germany) 1787-1854 | Michael Faraday (England) 1791-1867 | Friedrich Wilhelm Georg Kohlrausch (Germany) 1840-1910 |
GENERALITA'
Definizioni:Q |
Quantità di carica elettrica misurata in Coulomb C (1C = carica di 6.2415093×1018 elettroni; la carica di un elettrone = 1.602×10-19 C ) |
i = Q/t |
Intensità della corrente elettrica, misurata in Ampère (A). Un ampère equivale al passaggio della carica di un Coulomb in un secondo attraverso la sezione di un materiale conduttore (A= C sec-1) |
V |
Differenza di potenziale elettrico misurato in Volt (V) |
R |
Resistenza elettrica misurata in (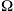 Ohm) Ohm) |
Secondo la prima legge di Ohm (1827), l'intensità della corrente elettrica che attraversa un conduttore (cioè la quantità di carica elettrica che attraversa una sua sezione in un secondo) è funzione diretta della differenza di potenziale (d.d.p.) applicata ai suoi capi e risulta inversamente proporzionale alla resistenza del conduttore stesso (vedi prima equazione in fig. seguente).
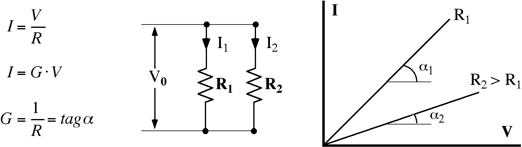 |
In termini qualitativi, si può pensare alla resistenza elettrica come quella proprietà che esprime l'opposizione del materiale a farsi attraversare dalla corrente elettrica.
La resistenza elettrica si misura in Ohm (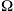 ). Un conduttore presenta la resistenza di 1 Ohm quando permette il passaggio di 1 Ampere di corrente elettrica se si applica una d.d.p. di 1 Volt ai suoi capi (i=V/R ne segue che R=V/i per cui 1
). Un conduttore presenta la resistenza di 1 Ohm quando permette il passaggio di 1 Ampere di corrente elettrica se si applica una d.d.p. di 1 Volt ai suoi capi (i=V/R ne segue che R=V/i per cui 1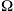 =1V/1A).
=1V/1A).
Si può definire un'altra grandezza: la Conduttanza. La conduttanza, usualmente indicata con la lettera C o G, equivale al reciproco della resistenza:
Questa grandezza esprime, pertanto, la capacità di un materiale,
in virtù della sua costituzione interna, a farsi attraversare dalla corrente elettrica. La sua unità di misura viene espressa in Ohm reciproci o Siemens (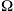 -1
= S).
-1
= S).
Tipi di conduttori:
Definiamo due
tipi di conduttori: quelli di prima e quelli di
seconda specie.
Quelli di prima specie sono i conduttori metallici
nei quali i portatori di carica sono gli elettroni. In essi la corrente elettrica si configura
come un flusso ordinato di elettroni in senso opposto alla
direzione del campo elettrico applicato (gli elettroni hanno carica negativa).
A temperature ordinare e costanti questo tipo di conduttori rispettano la prima legge di Ohm.
Quelli di seconda specie sono le soluzioni elettrolitiche. In questo caso i portatori di carica sono
gli ioni "liberi" rispetto alla posizione obbligata nei reticoli cristallini solidi. Oltre alla carica (positiva o negativa) gli ioni posseggono una massa spesso considerevole.
In questo tipo di conduttori la corrente elettrica si configura come un doppio movimento di ioni (associati ad un certo numero di molecole di solvente) diretti con verso opposto a seconda del segno della carica da essi posseduta.
La seconda legge di Ohm
Esprime la Resistenza in funzione della geometria tridimensionale del materiale in uso. Afferma che la resistenza elettrica è proporzionale alla lunghezza ed inversamente proporzionale alla sezione del conduttore (paragone idraulico)
 |
La costante di proporzionalità 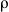 (rho)
è la resistenza dell'unità di materiale, ed
è detta quindi resistenza specifica
o Resistività del materiale. Per rapportarsi
meglio alle dimensioni dei materiali usati, talvolta non
vengono utilizzate le unità fondamentali per
esprimere la lunghezza e la sezione, preferendo ad esempio il centimetro al metro.
In tal caso la resistenza specifica:
(rho)
è la resistenza dell'unità di materiale, ed
è detta quindi resistenza specifica
o Resistività del materiale. Per rapportarsi
meglio alle dimensioni dei materiali usati, talvolta non
vengono utilizzate le unità fondamentali per
esprimere la lunghezza e la sezione, preferendo ad esempio il centimetro al metro.
In tal caso la resistenza specifica:
viene espressa in 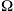 .cm (in
.cm (in 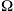 .m nel Sistema internazionale)
.m nel Sistema internazionale)
In elettrochimica spesso si preferisce utilizzare la conduttanza al posto della resistenza e, di conseguenza, la conduttanza specifica (γ = "gamma") al posto della resistenza specifica:
La conduttanza specifica γ, detta anche Conduttività (o talvolta, impropriamente a mio parere, Conducibilità), è l'inverso della resistenza
specifica e rappresenta quindi la conduttanza
dell'unità di materiale. La sua unità di misura usualmente è ![]() -1.cm-1
o S.cm-1 (Sistema internazionale:
-1.cm-1
o S.cm-1 (Sistema internazionale: ![]() -1.m-1 o S.m-1 )
-1.m-1 o S.m-1 )
Soluzioni di elettroliti
Si definiscono elettroliti tutte quelle specie chimiche che in soluzione, per interazione con il solvente, portano allla formazione di entità dotate di carica elettrica definite come ioni (La dissociazione elettrolitica secondo Arrhenius). (i biologi sono interessati soprattutto alle soluzioni acquose, i chimici non hanno preferenze).
Ecco alcuni esempi di sostanze classificate in base alla capacità di produrre ioni in soluzione acquosa (vedi esempio illustrativo):
Elettroliti forti: HCl(s) + H2O H+(aq.) + Cl-(aq.)
NaCl(s) + H2O Na+(aq.) + Cl-(aq.)
CaCl2(s) + H2O Ca++(aq.) + 2 Cl-(aq.)
Elettroliti deboli CH3COOH(aq.) CH3COO-(aq.) + H+(aq.)
HNO2(aq.) NO2-(aq.) + H+(aq.)
HClO2(aq.) ClO2-(aq.) + H+(aq.)
Non elettroliti: C6H12O6(aq.) , C2H5OH(aq.)
Una sostanza che si comporta da elettrolita "forte", appena viene sciolta in soluzione,
viene dissociata per interazione con il solvente quasi totalmente in ioni, moltiplicando per un
coefficiente intero (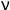 ) la
concentrazione in particelle estranee al solvente rispetto a quella prevista in
caso non si verificasse la dissociazione. Con (
) la
concentrazione in particelle estranee al solvente rispetto a quella prevista in
caso non si verificasse la dissociazione. Con (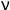 ) indichiamo
pertanto il numero di particelle che si formano a partire da una molecola di elettrolita.
Così, ad esempio, per NaCl
) indichiamo
pertanto il numero di particelle che si formano a partire da una molecola di elettrolita.
Così, ad esempio, per NaCl 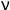 =2 mentre per CaCl2
=2 mentre per CaCl2 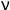 =3.
=3.
Nel caso di un elettrolita "debole", la produzione di ioni risulta inferiore rispetto agli elettroliti "forti" (dissociazione parziale secondo Arrhenius) e l'incremento del numero di particelle presenti in soluzione ed estranee al solvente dipende dal grado di reazione dell'elettrolita con il solvente (grado di dissociazione secondo Arrhenius).
Il grado di dissociazione, usualmente indicato con la lettera greca "α",
quando non viene espresso in termini percentuali, è inteso come il rapporto tra il numero di molecole dissociate e quelle presenti nel caso in cui non si verificasse dissociazione (ovvero le molecole inizialmente immesse in soluzione). In virtù di questa definizione, il numero "α" può assumere valori nell'intervallo (0 ÷ 1); tale valore, se moltiplicato per 100 indica la percentuale di molecole dissociate e assume valori nell'intervallo (0 ÷ 100). Il valore nullo si riferisce ai non elettroliti. Valori via via crescenti di α indicano elettroliti che vengono dissociati sempre di più fino al valore limite unitario che indica dissociazione totale.
In termini di frazione (num moli iniziali / num. moli iniziali) la quantità di soluto iinizialmente immesso in soluzione (il 100%), possiamo schematizzare il processo di dissociazione nel modo seguente:
AB 
A+ + B- n.mol iniz. / n.mol iniz. (fraz. iniziale) 1 - - n.mol diss. / n.mol iniz. (fraz. dissociata) α - - n.mol formate / n.mol iniz. (fraz. formate) - α α n.mol all'equil. / n.mol iniz. (fraz. all'equil.) 1 - α α α per generica C0 (moli per unità di volume) C0 (1-α) C0 α C0 α
La relazione esistente tra il grado di dissociazione di un elettrolita binario AB e la costante di equilibrio, ricavabile mediante il consueto schema utilizzato per gli equilibri, è la seguente:
 L'equazione scritta stabilisce la relazione tra la Kc, la concentrazione dell'elettrolita e il grado di dissociazione. Risolvendo rispetto ad alfa, si può verificare che il grado di dissociazione tende ad aumentare
per soluzioni via via meno concentrate ovvero più diluite (legge di diluizione
di Ostwald: Friederich Wilhelm Ostwald, 2/9/1853 - 4/4/1932, Riga, Lituania. Premio Nobel per la chimica 1909). Al limite, per diluizioni infinite, il grado di
dissociazione degli elettroliti, anche se deboli, raggiunge il valore
unitario (dissociazione completa). Nel plotting che segue ho rappresentato la
dipendenza del grado di dissociazione di un elettrolita binario AB dalla sua
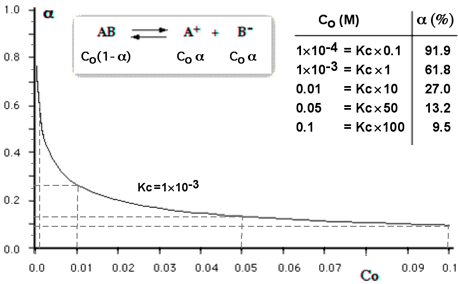
concentrazione; il grafico si riferisce ad un elettrolita binario con Kc = 0.001 (elettrolita debole ma non troppo) e la funzione è stata estesa fino alla concentrazione 0.1 Molare. La tabella sul lato destro del grafico indica il grado di dissociazione α (espresso in termini percentuali) in relazione alla concentrazione analitica dell'elettrolita C0 ; il valore di C0 viene rapportato al valore della Kc (il rapporto C0/Kc ampiamente esteso tra 0.1 e 100), pertanto, produce valori percentuali di α validi per qualunque valore di Kc.
L'equazione scritta stabilisce la relazione tra la Kc, la concentrazione dell'elettrolita e il grado di dissociazione. Risolvendo rispetto ad alfa, si può verificare che il grado di dissociazione tende ad aumentare
per soluzioni via via meno concentrate ovvero più diluite (legge di diluizione
di Ostwald: Friederich Wilhelm Ostwald, 2/9/1853 - 4/4/1932, Riga, Lituania. Premio Nobel per la chimica 1909). Al limite, per diluizioni infinite, il grado di
dissociazione degli elettroliti, anche se deboli, raggiunge il valore
unitario (dissociazione completa). Nel plotting che segue ho rappresentato la
dipendenza del grado di dissociazione di un elettrolita binario AB dalla sua
concentrazione; il grafico si riferisce ad un elettrolita binario con Kc = 0.001 (elettrolita debole ma non troppo) e la funzione è stata estesa fino alla concentrazione 0.1 Molare. La tabella sul lato destro del grafico indica il grado di dissociazione α (espresso in termini percentuali) in relazione alla concentrazione analitica dell'elettrolita C0 ; il valore di C0 viene rapportato al valore della Kc (il rapporto C0/Kc ampiamente esteso tra 0.1 e 100), pertanto, produce valori percentuali di α validi per qualunque valore di Kc.
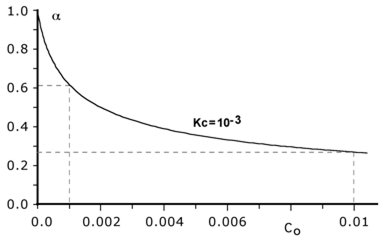
Il grafico seguente è lo stesso del precedente ma riporta la scala delle concentrazioni dell'elettrolita in un intervallo più ristretto (da zero a 0.01 molare):
La forza di un elettrolita, in virtù del fatto che l'entità della dissociazione (il grado di dissociazione) dipende dalla sua concentrazione, allo scopo di poter effettuare confronti inequivocabili tra elettroliti diversi, viene espressa dal valore della costante di dissociazione dell'elettrolita nello specifico solvente.
NOTA: Una sostanza, quando è "sciolta" in un solvente, subisce la sua aggressione chimica che induce, con modalità diverse per sostanze diverse, la separazione in ioni. In pratica non si tratta di semplice dissociazione ma di una reazione con il solvente che, per motivi di semplicità e per la sua picolissima variazione spesso non si trascrive negli schemi. In realtà anche il solvente subisce modificazioni a causa del soluto nonostante quest'ultimo sia presente in piccola quantità. In altri termini si potrebbe parlare di grado di reazione al posto di grado di dissociazione.
Proprietà colligative ed elettroliti
Come è noto le proprietà colligative dipendono dal numero di particelle in soluzione e non dal loro tipo. Nel caso di una specie che viene dissociata dal solvente o produca ioni (un elettrolita), si verifica un aumento della concentrazione in particelle. Questo fatto induce un'alterazione nel valore della proprietà rispetto al caso in cui non si ipotizzi il fenomeno dissociativo o produzione di ioni. Nel caso di un elettrolita forte (la cui dissociazione può essere considerata completa) la concentrazione totale in particelle sarà data dalla concentrazione formale dell'elettrolita moltiplicata per il coefficiente 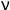 . Nel caso
di un elettrolita debole, la concentrazione totale in
particelle è data dalla somma della concentrazione di
tutte le specie, compresa quella parte rimasta indissociata. Per il semplice caso su riportato di un elettrolita
binario AB per il quale
. Nel caso
di un elettrolita debole, la concentrazione totale in
particelle è data dalla somma della concentrazione di
tutte le specie, compresa quella parte rimasta indissociata. Per il semplice caso su riportato di un elettrolita
binario AB per il quale 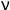 =2, la concentrazione totale in particelle sarà:
=2, la concentrazione totale in particelle sarà:
| C = C0 ( 1 - α) + C0 α + C0 α = C0 ( 1 + α) |
Per il generico elettrolita che produce 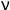 particelle ioniche, la concentrazione totale in particelle
è data dall'espressione:
particelle ioniche, la concentrazione totale in particelle
è data dall'espressione:
| C = C0 [ 1 + (ν - 1) α] |
La precedente espressione ha un carattere generale ed è valida sia per elettroliti forti (α = 1) che deboli (0 < α < 1) e persino per i non elettroliti (α = 0).
Alla luce di quanto detto le proprietà colligative vanno corrette con il cosiddetto coefficiente di van't Hoff (i) nel modo seguente:
| a) | ΔTcr = Kcr m i = Kcr m [ 1 + (ν - 1) α] |
| b) | ΔTeb = Keb m i = Keb m [ 1 + (ν - 1) α] | |
| c) | π = i M R T = [ 1 + (ν - 1) α] M R T |
Le precedenti espressioni forniscono l'opportunità, qualora sia misurata sperimentalmente la proprietà colligativa in questione, di calcolare il grado di dissociazione dell'elettrolita stesso.
ESEMPIO:
Una soluzione acquosa 0.1 molare di un acido debole HA
presenta, alla temperatura di 25.0°C, una pressione osmotica pari a 2.65 atmosfere. Calcolare il grado di dissociazione
dell'acido.
SOLUZIONE:
L'acido debole è parzialmente dissociato secondo lo
schema AB![]() A+
+ B- quindi il coefficiente i = (1 - α)
+ α + α =
1 + α. Risolvendo dall'espressione c) rispetto ad i, si ottiene
A+
+ B- quindi il coefficiente i = (1 - α)
+ α + α =
1 + α. Risolvendo dall'espressione c) rispetto ad i, si ottiene
| i = π / (M R T ) = 1 + α | ||
| da cui | ||
| α = π / (M R T ) - 1 = 2.65/(0.1*0.0821*298.15) - 1 = 0.083 |